인공지능 모형 만들기

선형모형의 구성

파이토치 레이어를 이용해서 회귀모형을 적합하는 코드를 작성해보겠습니다. 먼저 실습을 위해서 데이터를 생성해보겠습니다. $x$ 는 행이 20개 열이 5개인 설명변수고, $y$ 는 행이 20개 열이 1개인 반응변수입니다. 일반적으로 $x$는 관측치 1개가 5개의 변수를 가지고 있고, 총 20개의 관측치가 있는 테이블 데이터를 나타냅니다. 참 회귀가중치는 $(1.5, -2.0, 3.0, -1.0, 2.0)$ 인 5행 1열인 행렬로 놓았았고 상수항은 4로 놓았습니다. 관측치는 회귀모형에 표준정규분포의 오차를 더하여 만들었습니다.

# 임의의 데이터 생성
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

torch.manual_seed(0)
x = torch.randn(20, 5)  # 입력 데이터 (20, 5)
true_weights = torch.tensor([1.5, -2.0, 3.0, -1.0, 2.0]).unsqueeze(1)  # 실제 가중치
y = x @ true_weights + 4 + torch.randn(20, 1)  # 출력 데이터 (20, 1) 

다음으로 nn.Linear() 함수를 이용해서 5차원에서 1차원으로 변환되는 함수를 만들어보겠습니다. 여기서 만들어진 변수(함수)인 model을 확인하보세요.

# 선형모형의 구성
model = nn.Linear(5, 1)  # 입력 차원 5, 출력 차원 1

model 은 5차원 (변수가 5개인) 데이터를 1차원으로 변환하는 함수입니다. model 에 앞서 만든 x 를 입력하여 데이터가 변환되는지 확인해봅시다.

# 선형모형의 구성
model(x)

만들어진 model 함수는 parameter (회귀계수 및 상수항의 초기값)를 가지고 있습니다. model 이 만들어질때 모형을 정의하는 parameter가 초기화 됩니다. 이 parameter 는 다양한 방법으로 초기화 할 수 있습니다. 초기화 방법은 nn.init 모듈을 참조하기 바랍니다. 여기서는 먼저 model 의 회귀계수항과 상수항을 확인해봅시다.

# 모형 계수의 확인
# 회귀계수
print(model.weight)
# 상수항
print(model.bias)

parameter 값을 변경해보겠습니다. 여시서 with torch.no_grad() 는 자동미분 기능을 비활성화한 채로 값을 변경하기 위해 사용하였습니다.

# 모형 parameter의 변경
with torch.no_grad():
    model.weight = nn.Parameter(torch.tensor([[1.5, -2.0, 3.0, -1.0, 2.0]]))
    model.bias = nn.Parameter(torch.tensor([4.0]))

우리는 model 함수를 이용해서 반응변수의 추정치인 $\widehat{y}$ 을 만들 수 있게 되었습니다. $\widehat{y}$ 은 model(x)로 만들어 집니다.

손실함수의 설정과 모형의 학습

우리가 만든 model 함수는 parameter 가 초기화 되어 있지만, 이 parameter 는 임의로 설정된 것으로 좋은 예측성능을 가진 모형이라 할 수 없습니다. 데이터를 이용하여 이 parameter를 학습하는 과정에 대해 설명합니다. 먼저 예측치와 참값의 차이를 계산하는 손실함수를 설정합니다. 이어서 손실함수를 학습하는 최적화방법을 설정합니다.

nn.MSELoss 는 제곱손실함수로 최소제곱법을 통한 모형학습에 이용됩니다. optim.SGD(model.parameters(), lr=0.01) 는 model 함수가 가진 parameter, bias 함 (model.parameters())을 확률적경사하강법 (Stochastic Gradient Descent Method) 로 학습률 (learning rate) 0.01 로 갱신하겠다는 뜻입니다.

# 손실함수의 설정
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

다음은 반복문을 통해 model.parameters() 를 업데이트하는 과정을 나타냅니다.
- num_epochs = 1000 는 model.parameters() 를 업데이트하는 횟수를 나타냅니다.
- model.train() 는 모형의 적합시 훈련모드로 전환하여 미분값을 계산할 준비를 하도록 합니다.
- optimizer.zero_grad() 는 optimizer 내부에 저장된 미분값 저장공간의 값을 0으로 초기화 시켜 줍니다.
- outputs = model(x) 는 모형에 입력값을 넣서 출력값을 만들어 outputs 변수 로 저장합니다.
- loss = criterion(outputs, y) 앞서 설정한 손실함수 (criterion = nn.MSELoss()) 를 이용하여 모형출력값인 outputs과 데이터 참값인 y 를 비교하여 차이를 계산합니다. loss 는 텐서이며 이를 만드는 과정에 포함된 parameter 들로 자동미분이 가능한 객체입니다.
- loss.backward()는 자동미분 기능을 통하여 loss 의 미분값을 계산하는 과정입니다. loss 가 자동미분 기능을 가진 텐서 임을 다시 확인해보세요.
- optimizer.step() 는 정해진 optimizer (optimizer = optim.SGD(model.parameters(), lr=0.01))에 따라 model의 모형계수가 업데이트 됩니다.

# 모형의 학습
num_epochs = 1000
model.train() # 학습 모드로 전환
for epoch in range(num_epochs):
    optimizer.zero_grad()  # 그래디언트 초기화

    outputs = model(x)  # 모델 예측
    loss = criterion(outputs, y)  # 손실 계산
    loss.backward()  # 역전파
    optimizer.step()  # 옵티마이저 업데이트

    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

아래 코드를 이용하여 모형의 예측값과 학습계수를 확인할 수 있습니다.

# 학습 후 모델 파라미터
with torch.no_grad():
    weights = model.weight.data
    bias = model.bias.data
    print(f'Final model parameters: Weights = {weights}, Bias = {bias}')

# 결과 시각화
model.eval() # 모델 평가모드로 전환
with torch.no_grad():
    predicted = model(x)

# 데이터 시각화
plt.figure(figsize=(10, 6))
plt.scatter(predicted.numpy(), y.numpy(), label='Scatter Plot')
plt.xlabel("predicted")
plt.ylabel("true")
plt.show()

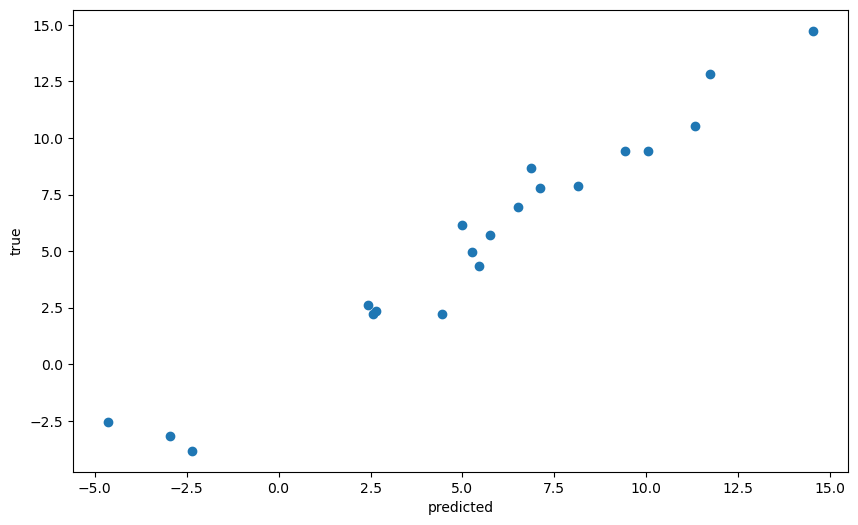
다음은 반응변수가 3차원인 회귀모형에 대한 적합예제를 보여줍니다. 이 예제를 통해 1) model 함수 구성 2) 손실함수의 설정 3) 최적화방법의 결정 4) 모형의 적합으로 이루어지는 절차의 편리성에 대해서 생각해봅시다.

# 3차원 반응변수를 가지는 선형회귀모형의 적합
# 임의의 데이터 생성
torch.manual_seed(0)
x = torch.randn(20, 5)  # 입력 데이터 (20, 5)
true_weights = torch.tensor([[1.5, -2.0, 3.0, -1.0, 2.0],
                              [2.0, -1.5, 1.0, -0.5, 3.0],
                              [1.0, -1.0, 2.5, -2.0, 1.5]])  # 실제 가중치 (3, 5)
y = x @ true_weights.t() + torch.tensor([4.0, -2.0, 1.0]) + torch.randn(20, 3)  # 출력 데이터 (20, 3)

# 선형 회귀 모델 정의
model = nn.Linear(5, 3)  # 입력 차원 5, 출력 차원 3

# 손실 함수와 옵티마이저 정의
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 학습 과정
num_epochs = 1000
model.train()
for epoch in range(num_epochs):
    optimizer.zero_grad()  # 그래디언트 초기화

    outputs = model(x)  # 모델 예측
    loss = criterion(outputs, y)  # 손실 계산
    loss.backward()  # 역전파
    optimizer.step()  # 옵티마이저 업데이트

    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 결과 시각화
model.eval()
with torch.no_grad():
    predicted = model(x)

# 데이터 시각화
plt.figure(figsize=(10, 15))
for i in range(3):
    plt.subplot(3, 1, i+1)
    plt.scatter(predicted[:, i].numpy(), y[:, i].numpy(), label=f'Original data (output {i+1})')
    plt.xlabel("predicted")
    plt.ylabel("true")
plt.tight_layout()
plt.show()  

로지스틱 회귀모형

로지스틱 회귀모형은 선형모형의 형태화 거의 유사하나 마지막 출력값의 형태가 0과 1 사이 숫자려 변환되는 과정이 있습니다. 여기서는 잠시 상수항을 무시하고 회귀모형을 설정하겠습니다. 0과 1사이의 예측값 \(\widehat{y} \) 는 다음과 같습니다. \[ \widehat{y} = \frac{\exp(X\beta)}{1 + \exp(X\beta)}\] 이는 \(\exp(X\beta)\) 를 시그모이드 함수 $\sigma(z) = \exp(z)/ 1+ \exp(z)$ 에 합성하여 얻을 수 있습니다.

먼저 데이터를 생성해보겠습니다.

# 데이터 생성
from sklearn.datasets import make_classification  
X, y = make_classification(n_samples=100, n_features=5, 
          n_informative=2, n_redundant=0, random_state=0)
print(x.shape)
print(x)

make_classification 함수는 간단하게 분류문제를 적합해보기 위해 샘플을 만드는 것입니다. 자세한 내용은 아래와 같습니다.
- n_classes = 2: (기본) 생성되는 반응변수의 클래스 수를 설정합니다.
- n_samples=100: 생성할 샘플의 수를 지정합니다. 여기서는 100개의 샘플을 생성합니다.
- n_features=5: 각 샘플의 특성(feature) 수를 지정합니다. 여기서는 5개의 특성을 갖는 샘플을 생성합니다.
- n_informative=2: 실제로 유의미한(informative) 특성의 수를 지정합니다. 무작위 선형조합을 통해 모형이 만들어집니다.
- n_redundant=0: 다른 특성의 선형 조합으로 생성되는 특성의 수를 지정합니다. 여기서는 0으로 설정되어 있으므로, 추가로 생성되는 특성은 없습니다.
- random_state=0: 난수 생성기의 시드를 설정합니다. 동일한 시드 값을 사용하면 항상 동일한 데이터셋이 생성됩니다. 재현 가능성을 위해 사용합니다.

참조: 만약 train, test 데이터를 나누고 싶은 경우에는 train_test_split 함수를 사용하면 됩니다.

# 데이터 생성 (훈련, 시험데이터 구분)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(n_samples=100, n_features=5, 
        n_informative=2, n_redundant=0, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)  

make_classification 을 통해 만들어진 데이터는 numpy 행렬입니다. 이를 파이토치 모형의 입력값인 tensor 로 변환하기 위해서는 torch.tensor 를 이용합니다. 데이터 형식의 지정에 유의하세요. y값은 unsqueeze(1) 로 행렬형태로 변환하고 있음을 살펴보세요.

# 텐서 변환
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32).unsqueeze(1)  

딥러닝의 모형 적합에 사용하는 pytorch 패키지는 모형 내부의 연산을 위해 tensor 라는 특별한 변수로 데이터를 읽습니다. 파이썬에서 외부에서 데이터를 읽거나 내부에서 데이터를 생성하는 경우 pandas.DataFrame 형식이나 numpy.array 형식의 데이터를 사용하기 때문에 pytorch 에서 사용하는 tensor 로 데이터 변환이 이루어져야 합니다. 여기서는 먼저 텐서의 형식을 가지는 데이터를 만들어 보고, numpy.array 데이터를 tensor 로 변환하는 방법을 알아보겠습니다.

먼저 모든 값이 0 인 5행 3열 텐서를 만들어 봅니다. torch.zeros 함수를 사용하면 만들 수 있습니다.

# nn.Sequential을 사용하여 로지스틱 회귀 모델 정의
model = nn.Sequential(
    nn.Linear(5, 1),
    nn.Sigmoid())

# 손실 함수와 옵티마이저 정의
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 학습 과정
num_epochs = 1000
model.train()
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(X)
    loss = criterion(outputs, y)
    loss.backward()
    optimizer.step()
    
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 학습 후 모델 평가
model.eval()
with torch.no_grad():
    predicted = model(X).round()
    accuracy = (predicted.eq(y).sum().item() / y.shape[0]) * 100
    print(f'Accuracy: {accuracy:.2f}%')

다항로지스틱 회귀모형

다음은 다중 분류 문제입니다. 여기서는 CrossEntropyLoss 가 가지고 있는 softmax 변환에 sigmoid 함수 변환이 포함되어 있습니다. 그래서 model 을 구성할 때 Sigmoid 함수를 사용하지 않습니다. y 의 데이터 형에 주목하세요. 우리가 사용한 모형은 y가 class 의 번호를 나타내는 정수형으로 표현되어 있으면 됩니다. 원-핫 벡터로 변환하지 않아도 됩니다.

# 데이터 생성
X, y = make_classification(n_samples=200, n_features=20, 
                        n_informative=10, n_redundant=0, 
                        n_classes=5, random_state=0)
# 데이터를 텐서로 변환
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.int64)

# nn.Sequential을 사용하여 다중 클래스 로지스틱 회귀 모델 정의
model = nn.Sequential(nn.Linear(20, 5))  # 입력 차원이 20이고, 출력 차원이 5인 선형 레이어

# 손실 함수와 옵티마이저 정의
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 학습 과정
num_epochs = 1000
model.train()
for epoch in range(num_epochs):
    optimizer.zero_grad()  # 그래디언트 초기화

    outputs = model(X)  # 모델 예측
    loss = criterion(outputs, y)  # 손실 계산
    loss.backward()  # 역전파
    optimizer.step()  # 옵티마이저 업데이트

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 학습 후 모델 평가
model.eval()
with torch.no_grad():
    outputs = model(X)
    _, predicted = torch.max(outputs, 1)
    accuracy = (predicted == y).sum().item() / y.size(0) * 100
    print(f'Accuracy: {accuracy:.2f}%')  

아래는 모형의 학습에 정규화 과정을 추가하는 예를 보여줍니다. StandardScaler 를 이용하여 scaler 함수를 만들었고 fit_transform 내장함수를 이용해서 정규화를 하였습니다. 신경망 모형에서 모형이 복잡해질때 데이터 정규화는 모형의 적합이 더 잘 이루어지도록 만들어 줍니다.

model = nn.Sequential(nn.Linear(20, 5)) 은 입력데이터 내 변수의 개수가 20개 (20차원)인데 그것을 선형변환을 통해서 5개 변수로 줄인다는 뜻입니다. 이를 5차원 feature vector라 부르기도 합니다. 그 이후 과정은 이진 분류 로지스틱모형 코드와 거의 유사합니다.

# 정규화 과정의 추가
from sklearn.preprocessing import StandardScaler
X, y = make_classification(n_samples=200, n_features=20, 
                        n_informative=10, n_redundant=0, 
                        n_classes=5, random_state=0)
# 정규화 과정의 추가
scaler = StandardScaler()
X = scaler.fit_transform(X)
# 데이터를 텐서로 변환
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.int64)
# nn.Sequential을 사용하여 다중 클래스 로지스틱 회귀 모델 정의
model = nn.Sequential(nn.Linear(20, 5))  # 입력 차원이 20이고, 출력 차원이 5인 선형 레이어


# 손실 함수와 옵티마이저 정의
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 학습 과정
num_epochs = 1000
model.train()
for epoch in range(num_epochs):
    optimizer.zero_grad()  # 그래디언트 초기화

    outputs = model(X)  # 모델 예측
    loss = criterion(outputs, y)  # 손실 계산
    loss.backward()  # 역전파
    optimizer.step()  # 옵티마이저 업데이트

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')
  

다항로지스틱 신경망 모형

복잡한 신경망 모형을 만들어 보겠습니다. 여기서는 Feed Forward Neural Network를 모형화 하는 데, 이 신경망 모형은 (선형변환, 비선형변환)의 함성함수로 만듭니다. 합성함수를 만들때 사용하는 함수는 nn.Sequential 입니다. nn.Linear 와 nn.Sigmoid 를 반복적으로 연결하여 여러개의 층을 가진 신경망 모형을 만들겠습니다. 데이터는 위 예제에서 만든 다항 로지스틱 회귀모형의 예제 데이터를 그대로 사용합니다.

# FFN 의 구성
model = nn.Sequential(nn.Linear(20,10),
        nn.Sigmoid(),
        nn.Linear(10,8),
        nn.Sigmoid(),
        nn.Linear(8,5),
        nn.Sigmoid(),
        nn.Linear(5,5))

print(model)

이 모형은 먼저 변수 20개 (20차원)이 10개로 선형변환되고, 시그모이드 함수로 비선형 변환이 이루어집니다. 다음은 줄어든 변수 10개가 5개로 줄고 비선형변환이 일어납니다. 마지막으로 변수 5개로 선형변환이 일어납니다. 이 값을 이용해 확률이 계산됩니다. 예측 확률은 아래와 같이 얻을 수 있습니다.

# 확률 출력값의 생성 
import torch.nn.functional as F
logits = model(X)
softmax_output = F.softmax(logits, dim=1)
softmax_output.argmax(dim=1) # 최대 확률값을 가지는 index 확인

이제 모형을 만들었으니 새로 학습을 해보겠습니다. 다항 로지스틱 모형의 적합에서 모형을 설정하는 부분을 제외하고 코드를 복사해서 실행해봅시다.

모형의 성능이 잘 안나올 경우에는 optimizer 를 변경할 수도 있습니다. 아래의 optimizer 를 재설정한 후 이전의 다항 로지스틱 모형의 적합에서 모형을 설정하는 부분과 optimizer 설정부분을 제외하고 코드를 복사해서 실행해봅시다. 실행해봅시다.

#optimziazer 의 재설정
optimizer = optim.Adam(model.parameters())

모형의 parameter 는 레이어 별로 확인이 가능합니다. model 을 프린트하면 레이어 인덱스와 레이어 형태를 확인할 수 있습니다. 가령 model[0] 을 지정하면 첫 번째 nn.Linear(20,10) 이 나올 것입니다. 모형 계수는 model[0].weight 와 model[0].bias 를 통해 확인할 수 있습니다.